Engineering and Technology Quarterly Reviews
ISSN 2622-9374




Published: 10 February 2021
Application of Uniformly Valid Shell Theory
Samuel W Chung, Hyun-ho Ju
University of Utah (USA), Dong Guk University (South Korea)
Download Full-Text Pdf
10.5281/zenodo.4529496
Pages: 10-23
Keywords: Shell Theory, circular cylindrical shell, applicability
Abstract
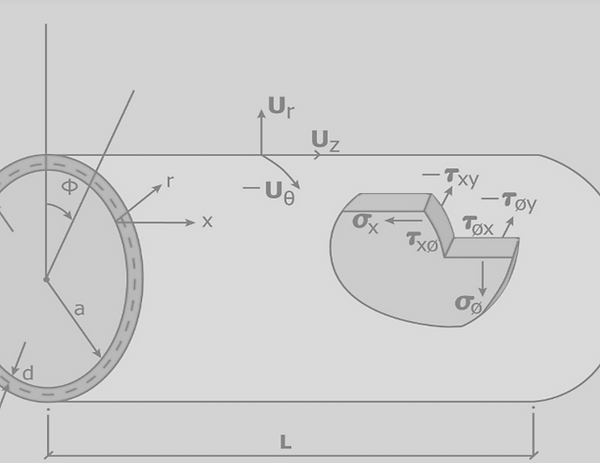
For the purpose of demonstrating the applicability of the previously derived theories, the problem of a laminated circular cylindrical shell under internal pressure and edge loadings will be examined. The cylinder is assumed to consist of boron/epoxy composite layers. Each layer is taken to be homogeneous but anisotropic with an arbitrary orientation of the elastic axes. We need not consider the restriction of the symmetry of the layering due to the non-homogeneity considered in the original development of the theory expressed by the constitutive equations. Thus, each layer can possess a different thickness.
References
LOVE, A. E. H., "A treatise on the mathematical theory of elasticity", Dover Edition, New York.
REISSNER, E., "The effect of transverse shear deformation on the bending of elastic plates", J. Appl. Mech. 12, Nos.A69-A77,(1945).
GOLDENVEISER, A. L., "Theory of elastic thin shells", Pergamon
REISSNER, E., "On some problems in shell theory", Proc. 1st Symposium on Naval Structural Mechanics (Stanford University),(1958).
REISSNER, E. and STAVSKY, Y., "Bending and stretching of certain types of heterogeneous aelotropic elastic plates", J. Appl. Mech.,Paper No. 61-APM-21,(1961).
DONG, R. G. and DONG, S. B., "Analysis of slightly anisotropic shells", AIAA Journal, 1, No.11, November,(1963).
WIDERA, 0. E. and CHUNG, S. W., "A theory for non-homogeneous anisotropic cylindrical shells", J. COMPOSITE MATERIALS, 6, January, (1972).
GOLDENVEISER, A. L., "Methods for justifying and refining the theory of shells", P.M.M. 32, 684 (1968).
JOHNSON, M. W. and REISSNER, E., "On the foundations of the theory thin elastic shells", J. Math. Phys. 37, 371 (1959).
REISS, E. L., "A theory for the small rotationally symmetric deformations of cylindrical shells". Communications on Pure and Applied Mathematics XIII, 531 (1960).
WILCOX, C. H., "Asymptotic solutions of differential equations and their applications", John-Wiley and.Sons, Inc..
VAN DYKE, M., "Pertubation methods in fluid mechanics", Academic Press, (1964).
DYM, C. L. and HOFF, N. J., "Pertubation-solutions for the buckling problem of axially compressed thin cylindrical shells", AFO SR-66--1755, SUDAAR No.282, Stanford University.
BERT, C. W., "Structural theory for laminated anisotropic elastic shells", J. COMPOSITE MATERIALS 1, 414 (1967).
VLASOV, V. Z., "General theory of shells and its applications in engineering", NASA TT F-99, National Tech. Information Service.
CHUNG, S.W., “A Comparison of Membrane Shell Theories of Hybrid Anisotropic Materials”, European Journal of Engineering and Technology, Volume 4, No.5,2016 http://www.idpublications.org/ejet-vol-4-no-5-2016/
Chung, S.W., Hong, S.G. and Ju, G.S., “Details of Semi-Membrane Shell Theory of Hybrid Anisotropic Materials” International Journal of Composite Materials 2018.8(3):47-56,
Chung, S.W., Hong, S.G., Ju, G.S. “Pure Membrane, Pseudo Membrane, and Semi Membrane Shell Theories of Hybrid Anisotropic Materials”, Journal of Material Science and Engineering A 8 (5-6) (2018) 121-135,
Chung, S.W., Hong, S.G., Ju, G.S., “Semi-Membrane and Effective Length Theory of hybrid Anisotropic Materials“, International Journal of Composite Materials. volume 7 (3), 2017: Contact Us: editor@sapub.org , ID:110900221
Chung, S. W.1, Hong S. G.2, Ju G. S.3, “Applications of Pure Membrane, Pseudo Membrane, and Semi Membrane Shell Theories of Hybrid Anisotropic Materials”, International Journal of Composite Materials p-ISSN: 2166-479X e-ISSN: 2166-4919, 2018; 8(4): 73-90 doi:10.5923/j.cmaterials.20180804.01
Chung S. W.1, Hong, S. G.2, Ju G. S.3,,“A Spherical Shell Theory of Hybrid Anisotropic Materials”. International Journal of Composite Materials p-ISSN: 2166-479X e-ISSN: 2166-4919 2018; 8(4): 97-104, ID:110900262, doi:10.5923/j.cmaterials.20180804.03
